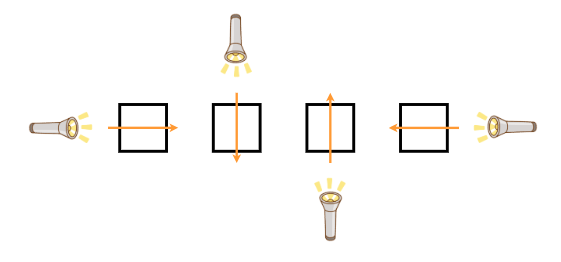题目

题目评级

A < B < C < E < D <<< F <<<<<<<<<<<<<< G

A.Robot Balance

题目描述

高桥可以将头部部件和身体部件组合成一个机器人。如果头部部件的重量大于身体部件的重量，机器人就会摔倒。

目前，他有一个头部部件和一个身体部件。头部的重量为 $H$ 克，身体部分的重量为 $B$ 克。

他想让身体部分更重一些，这样机器人就不会摔倒。求为了使机器人不倒下，身体部分需要再加重多少克？

思路

语法题

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
    int a, b;
    cin >> a >> b;
    cout << max(a - b, 0ll);
    return 0;
}

B.Robot Weight

题目描述

有一个机器人，初始重量为 $X$ 。该机器人可同时连接 $N$ 种零件： $1,$ 种 $2,\ldots,$ 种 $N$ 种。 $i\ (1\le i\le N)$ 型零件的重量为 $W _ i$ 。最初，机器人上没有安装任何 $N$ 类型的部件。

依次处理以下 $Q$ 查询。 $i$ -查询 $(1\le i\le Q)$ 用整数 $P _ i$ 表示，内容如下：

如果 $P _ i$ 型部件当前没有安装在机器人上，则将其安装上；如果已安装，则将其移除。然后，打印机器人当前的重量。

思路

语法题

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
    int x;
    cin >> x;
    int n;
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    int q;
    cin >> q;
    vector<int> vis(n + 1, 0);
    while (q--) {
        int tp;
        cin >> tp;
        x += (vis[tp] ? -1 : 1) * a[tp];
        vis[tp] = !vis[tp];
        cout << x << '\n';
    }
    return 0;
}

C.Robot Factory

题目描述

高桥可以将头部部件和身体部件组合成一个机器人。如果头部部件的重量大于身体部件的重量，机器人就会摔倒。

目前，他有 $N$ 个头部部件和 $M$ 个身体部件。头部 $i$ /- $(1\le i\le N)$ 的重量为 $H _ i$ 克，身体 $i$ /- $(1\le i\le M)$ 的重量为 $B _ i$ 克。

他希望通过适当组合他所拥有的部件，制造出总共 $K$ 个不会倒下的机器人。请判断他能否通过合理组合零件来实现目标。

在这里，一个部件不能用来制造多个机器人，两个或多个头部部件（或两个或多个身体部件）不能用来制造一个机器人。

思路

我们把 $A$ 和 $B$ 都排序。

我们只需要对于当前最小的未匹配的 $A_i$ 找到一个尽量小的 $B_i$ 和它匹配，答案应该就是最优的，如果当前的 $A_i$ 都无法匹配这个 $B_i$ ，后面的肯定也匹配不上。我们直接搞两个指针往后做就可以了。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
signed main()
{
    int n, m, k;
    cin >> n >> m >> k;
    vector<int> a(n), b(m);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    for (int i = 0; i < m; i++) {
        cin >> b[i];
    }
    sort(a.begin(), a.end());
    sort(b.begin(), b.end());
    int cnt = 0;
    int i = 0, j = 0;
    while (i < n && j < m) {
        if (a[i] <= b[j]) {  
            cnt++;
            i++;
            j++;
        } else {  
            j++;
        }
    }
    cout << (cnt >= k ? "Yes" : "No");
    return 0;
}

D.Robot Customize

题目描述

有一个由头部和身体组成的机器人。该机器人有 $N$ 种可同时连接的部件： $1,$ 种 $2,\ldots,$ 种 $N$ 。 $i\ (1\le i\le N)$ 型部件的重量为 $W _ i$ 。每个部分连接到头部和连接到身体时的**幸福感是不同的。当 $i\ (1\le i\le N)$ 型部件与头部相连时的幸福感为 $H _ i$ ，而与身体相连时的幸福感为 $B _ i$ 。

如果头部的重量大于身体的重量，机器人就会倒下。这里，头部重量和身体重量分别是连接头部或身体的各部分重量之和。

高桥希望在机器人上安装所有 $N$ 种零件，每种各一个。在不导致机器人倒下的情况下，求所有部件连接后的最大幸福值之和。

思路

显然的背包， $dp_{i,j}$ 表示前 $i$ 个零件，头部重量与身体重量的差值为 $j-250000$ 的最大幸福值。

这里 $j$ 可能是负数所以要这么定义，但是atc的题解好像比我的代码更清爽一点

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int dp[2][500005];
signed main()
{
    int n;
    cin >> n;
    vector<int> a(n), b(n), c(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i] >> b[i] >> c[i];
    }
    memset(dp, -1, sizeof(dp));
    dp[0][250000] = 0;
    for (int i = 0; i < n; i++) {
        memset(dp[!(i & 1)], -1, sizeof(dp[!(i & 1)]));
        for (int j = 0; j <= 500000; j++) {
            if (dp[i & 1][j] < 0) {
                continue;
            }
            if (j + a[i] >= 0 && j + a[i] <= 500000) {
                dp[!(i & 1)][j + a[i]] = max(dp[!(i & 1)][j + a[i]], dp[i & 1][j] + b[i]);
            }
            if (j - a[i] >= 0 && j - a[i] <= 500000) {
                dp[!(i & 1)][j - a[i]] = max(dp[!(i & 1)][j - a[i]], dp[i & 1][j] + c[i]);
            }
        }
    }
    int ans = -1;
    for (int j = 0; j <= 250000; j++) {
        if (dp[n & 1][j] >= 0) {
            ans = max(ans, dp[n & 1][j]);
        }
    }
    cout << ans;
    return 0;
}

E.Reflection on Grid

题目描述

问题陈述

有一个网格，网格中有 $H$ 行和 $W$ 列。我们将位于从上往下 $i$ 行和从左往上 $j$ 列的单元格称为单元格 $(i,j)$ 。每个单元格上最多有一面镜子。

高桥站在 $(1,1)$ 单元格的左边，青木站在 $(H,W)$ 单元格的右边。高桥拿着手电筒，从 $(1,1)$ 单元格的左侧向右侧照射。在此，假设手电筒的光线不会漫射，而是直射光线。

高桥的目标是通过网格中的镜子将手电筒的光线传递给青木。

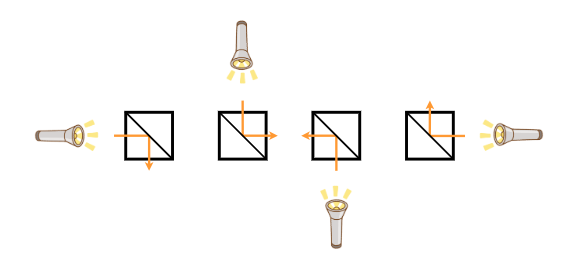
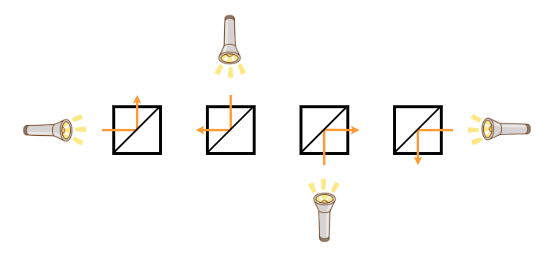
镜子的位置有三种。当光线照射到镜子上时，光线的方向会根据镜子的位置发生变化。对于每种镜面位置，每个入射方向的出射方向如下图所示。

类型 A（未放置反射镜）

B 型（在连接左上角和右下角的对角线上放置一面镜子）

C 型（在连接右上角和左下角的对角线上放置一面镜子）

网格上镜子的位置由长度为 $W$ 的 $H$ 字符串表示： $S_1,S_2,\ldots,S_H$ .当 $S_i$ 的 $j$ -th 字符为 "A "时，单元格 $(i,j)$ 为 A 类型；当为 "B "时，单元格 $(i,j)$ 为 B 类型；当为 "C "时，单元格 $(i,j)$ 为 C 类型。

高桥可以执行以下任意次数的操作，将光线传送给青木：

选择一个单元格，并将该单元格的镜面位置改为不同的类型。

求将光传送给青木所需的最少操作次数。

给你 $T$ 个测试案例，请找出每个案例的答案。

思路

感觉其实这题很显然，只是写代码有点恶心。

考虑最短路，每次BFS的时候存的信息包括横纵坐标、光线方向、距离。记一个距离数组满足 $dp_{i,j,k}$ 就是坐标 $(i,j)$ 光线方向为 $k$ 时的最优解。

这里可以01BFS 我赛时写了个dijkstra 思路很简单就是代码写起来比较恶心

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
void solve()
{
    int n, m;
    cin >> n >> m;
    vector<string> s(n);
    for (int i = 0; i < n; i++) {
        cin >> s[i];
    }
    vector<vector<vector<int>>> dp(n, vector<vector<int>>(m, vector<int>(4, INT_MAX)));
    priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;
    dp[0][0][0] = 0;
    pq.push({0, 0, 0, 0});
    int ans = INT_MAX;
    while (!pq.empty()) {
        auto u = pq.top();
        pq.pop();
        int c = u[0], x = u[1], y = u[2], d = u[3];
        if (c > dp[x][y][d]) {
            continue;
        }
        string ttp = "ABC";
        for (int i = 0; i < 3; i++) {
            int tp = d;
            if (ttp[i] == 'B') {
                if (d == 0) {
                    tp = 2;
                } else if (d == 1) {
                    tp = 3;
                } else if (d == 2) {
                    tp = 0;
                } else if (d == 3) {
                    tp = 1;
                }
            } else if (ttp[i] == 'C') {
                if (d == 0) {
                    tp = 3;
                } else if (d == 1) {
                    tp = 2;
                } else if (d == 2) {
                    tp = 1;
                } else if (d == 3) {
                    tp = 0;
                }
            }
            int dx = x + dir[tp][0];
            int dy = y + dir[tp][1];
            if (x == n - 1 && y == m - 1 && tp == 0) {
                ans = min(ans, c + ((ttp[i] != s[x][y]) ? 1LL : 0LL));
                continue;
            }
            if (dx >= 0 && dx < n && dy >= 0 && dy < m) {
                int nex = c + ((ttp[i] != s[x][y]) ? 1 : 0);
                if (dp[dx][dy][tp] > nex) {
                    dp[dx][dy][tp] = nex;
                    pq.push({nex, dx, dy, tp});
                }
            }
        }
    }
    cout << (ans == INT_MAX ? -1 : ans) << '\n';
}
signed main()
{
    int T;
    cin >> T;
    while (T--) {
        solve();
    }
    return 0;
}

复盘

G就是史 F看到样例过了就忘记乘上组合数系数结果AC7 WA30到比赛结束都没发现（