树状数组是什么

本质上就是一个长得像树的数组，长得很像一个二叉树，like下面的图：

1

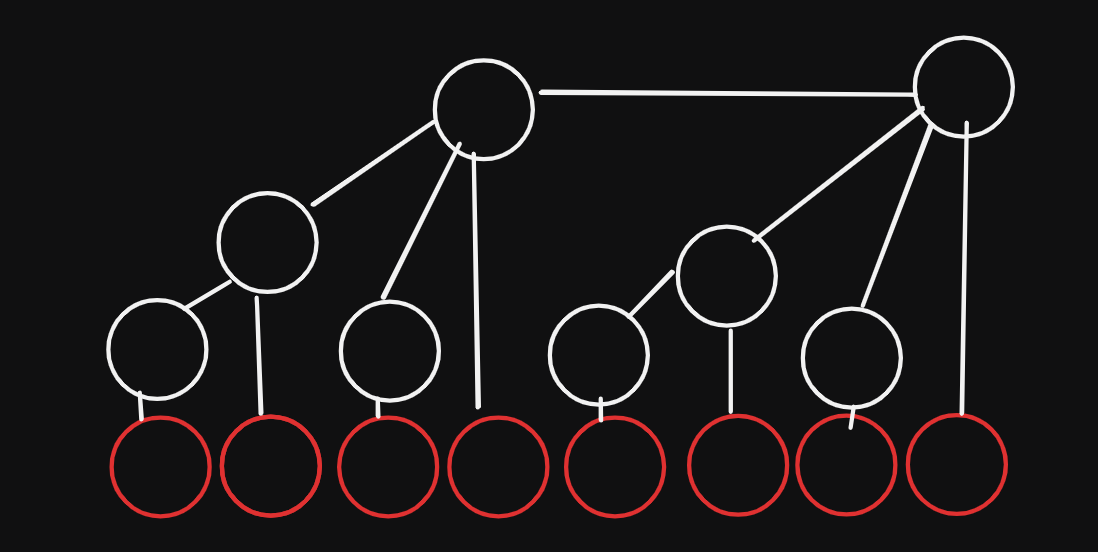
我们拿它干嘛呢？我们可以拿它来单点修改，区间查询。

那就有人说：欸，那线段树功能性比树状数组多，你怎么不用线段树？

你这么认这个功能性干嘛啊，它会把其他方面给异化掉的懂吗，知不知道什么叫异化跟具体化？

赛场上可能同一个问题树状数组要写10min，但是线段树要30min，你说你写那个？

怎么实现树状数组

好奇树状数组是怎么被人想出来的

lowbit

树状数组是通过这个叫lowbit的函数实现的，它主要用来求一个二进制数最低的一位11以及它后面的一堆00组成的数。

说具体点，比如说114114这个数，它就等于(1110010)2(1110010)_2，那求lowbit后就会变成(10)2(10)_2，也就是2

那想要求出lowbit函数的值，我们只需要让它返回xx andand (−x)(-x)就可以了

结构

还是那张图片，我们把数组从前往后编号，你会发现深度相同的位置二进制下末尾0的个数是相同的！

2

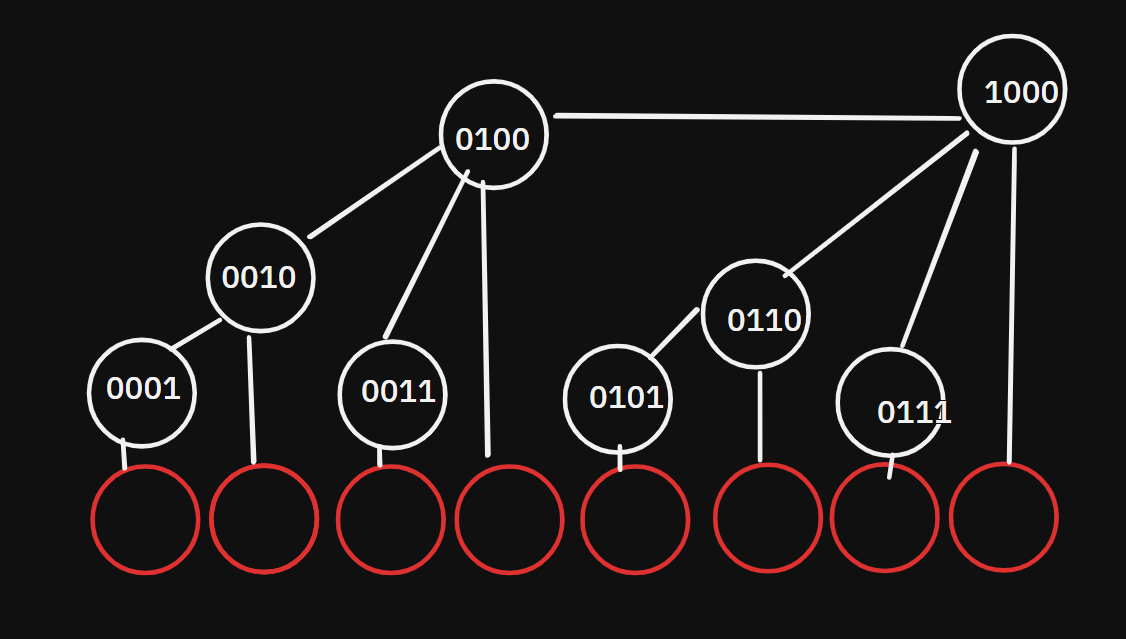
原理

比如我们想要求数组的前4项，那答案就是bit[4]=bit[4]=与它连接的bit[2]+bit[3]bit[2]+bit[3]，你可以试试其他的，你就会知道为什么这个数组要这样建立。

单点修改和区间查询

我们修改了这一个点之后，它和它的父节点都要改一下，所以代码应该是这样的：

1
2
3
4
5
6
int update(int pos, int k)
{
	for (int i = pos; i < n; i += lowbit(i)) {
        bit[pos] += k;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
int find(int l, int r)
{
	int ans = 0;
	for (int i = l - 1; i > 0; i -= lowbit(i)) {
	    ans -= bit[i];
    }
	for (int i = r; i > 0; i -= lowbit(i)) {
	    ans += bit[i];
    }
	return 0;
}

这里的函数实现用了类似前缀和的思路

区间修改和单点查询

这里区间修改并不好弄，我们可以用一个差分，类似这样：

1
2
update(l, k);
update(r + 1, -k);

那查询就变得简单了，我们输出前缀和就可以了。

1
2
3
4
5
6
7
8
9
int ask(int pos)
{
	int ans = 0;
	for (int i = pos; i > 0; i -= lowbit(i))  {
        ans += bit[i];
    }
	return ans;
}

区间修改和区间查询

好吧这里确实应该用线段树，因为树状数组扩展性并不好，所以比线段树都难写，等我马上写出线段树的笔记我会讲这个东西。

有兴趣可以自己探索

习题

洛谷P3347

洛谷P1908

ps：P1908其实有一种归并排序的简单做法，但是也可以用树状数组做。