今天是2025年2月12日,这是洛谷的占卜结果:

显然适合学习新算法,今天早上正好学了tarjan,来稍微写一写。
tarjan
tarjan求SCC
SCC是什么
度娘说了:
有向图强连通分量:在有向图G中,如果两个顶点Vi,Vj间(Vi>Vj)有一条从Vi到Vj的有向路径,同时还有一条从Vj到Vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)
用人话说,就是一个任意两个点可以互相到达的图就叫做强连通分量。
比如这个风韵犹存可爱的一张图:
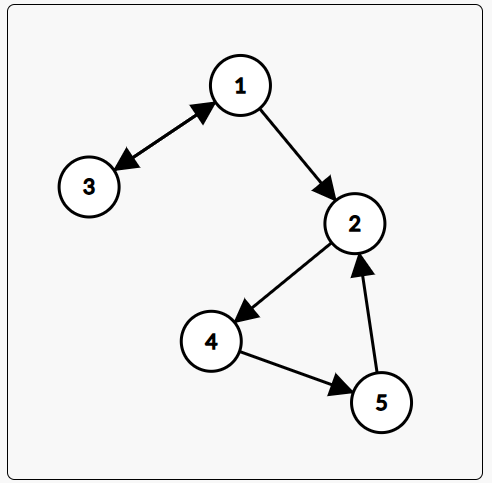
这里,点1,3可以互相到达,所以1,3这两个点构成了一个SCC。
点2,4,5也可以互相到达,所以2,4,5这三个点构成了一个SCC。
好了,我们知道要求的东西了,那来看看怎么求。
思路
其实tarjan说白了就是一个DFS,把图看作一个搜索树,每个SCC就是它的一个子树。
算法维护三个数组和一个栈:
说完了要用的数组我再来说一说主要的思路:
我们首先把dfn和low数组设置为当前的时间,把vis更新为1,把这个点放到栈里面。
我们把和当前点连出去的点遍历一遍,如果能继续搜下去就搜到底,我们每次搜完一个点时为了使low保持是最小的状态,要和自己的low和搜出去的点取最小值。
如果搜完所有连出去的点后发现dfn和low居然相等,那表示它的low压根没有更新过,就证明是搜索树中的根节点,这个时候我们就找完了一个SCC。
我们把SCC的计数加1,然后不断把栈pop,每一次把栈顶元素的vis改成0,并把所归属的SCC数组设置为当前的SCC的计数,直到栈顶和当前的元素相等就停下来。
这就是tarjan求SCC的详细思路,你看懂了吗?
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| void tarjan(int x)
{
vis[x] = 1;
cnt++;
dfn[x] = low[x] = cnt;
st.push(x);
for (int i = 0; i < edges[x].size(); i++) {
int nex = edges[x][i];
if (!dfn[nex]) {
tarjan(nex);
low[x] = min(low[x], low[nex]);
} else {
if (vis[nex]) {
low[x] = min(low[x], low[nex]);
}
}
}
if (dfn[x] == low[x]) {
cntscc++;
while (1) {
int tp = st.top();
st.pop();
scc[tp] = cntscc;
vis[tp] = 0;
if (tp == x) {
break;
}
}
}
}
|
tarjan缩点
什么?你说你还没看懂上面那个tarjan求SCC?
建议看懂上面再看下面,不然会吃大亏。
思路
缩点指的不是一种点,而是用tarjan求SCC的方法解决一类问题的一种思想(我的理解)。
来看一个板子问题:
给你一个n个点m条边的有向图(没错,我没说无环),问最少加上几条边可以做到让整个图变成SCC?
我们知道:一个DAG,如果想把它变成SCC,我们最少需要添加max(入度为0的点,出度为0的点)。
那问题就在于原题可能有环,因为环只可能在SCC中存在,而不会在SCC之间存在,所以我们可以把SCC求完之后把每个SCC看作一个点,然后问题不就解决了?
我上面说的这个做法,其实就是缩点的思想。
所以,没啥好说的了。
代码
代码其实没啥好放的
嗯,我们拿洛谷的那道板子来说吧,我们已经把所有的SCC编过号了,所以可以再建一个图,然后把所有起点和终点不在同一个SCC里面的边放到这个新图里面。
因为已经是DAG,跑一个可爱的拓扑排序就搞定了。
好了,你学会缩点了,可以去学2-SAT了
tarjan求割点
割点是什么
对于一个无向图,如果删除这个点之后图的SCC数量增加了,我们就称这个点为割点。
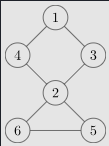
不难看出,2是这个图里唯一的割点。
思路
对于某个顶点u,如果至少存在一个u的儿子v使得lowv≤dfnu,也就是代表不能回到祖先,那这个u就是割点了。
当然这个方法对于我们一开始搜索的点就不适用了。如果这个点不是割点:那其他的路径也可以到达全部的节点,这表明这个点只有一个孩子。
反过来想,如果这个点有超过两个孩子且为一开始搜索的点,那也可以被判定为割点。
按照这个思路,用tarjan就可以轻松搞定了。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| #include<bits/stdc++.h>
using namespace std;
int dfn[111111], low[111111], scc[111111];
int scccnt, cnt, n, m;
bool vis[111111], flag[111111];
vector<int> edges[111111];
stack<int> st;
void tarjan(int x, int fa)
{
vis[x] = 1;
st.push(x);
cnt++;
dfn[x] = low[x] = cnt;
int ch = 0;
for (int i = 0; i < edges[x].size(); i++) {
int nex = edges[x][i];
if (!vis[nex]) {
ch++;
tarjan(nex, x);
low[x] = min(low[x], low[nex]);
if (fa != x && low[nex] >= dfn[x]) {
flag[x] = 1;
}
} else if (nex != fa) {
low[x] = min(low[x], dfn[nex]);
}
}
if (x == fa && ch >= 2) {
flag[x] = 1;
}
return;
}
int main()
{
cin >> n >> m;
for (int i = 0; i < m; i++) {
int u, v;
cin >> u >> v;
edges[u].push_back(v);
edges[v].push_back(u);
}
for (int i = 1; i <= n; i++) {
if (!dfn[i]) {
tarjan(i, i);
}
}
vector<int> ans;
for (int i = 1; i <= n; i++) {
if (flag[i]) {
ans.push_back(i);
}
}
cout << ans.size() << '\n';
for (int i = 0; i < ans.size(); i++) {
cout << ans[i] << ' ';
}
return 0;
}
|
tarjan求割边
割边是什么
和割点差不多。顾名思义,如果删掉这条边之后原图的SCC增加了,那么这条边就可以叫割边,也可以叫桥。
![g3][g3.png]
上图中红色的边就是割边。
思路
和割点也差不多,我们把dfnu≤lowv改为dfnu<lowv就可以了。
但是如果有重边的话这个思路就会挂了,因为如果两个节点之间有多条边的话,那这些重边都不能是割点。
我们可以通过把递归中fa这个参数改成刚刚走过的点的编号其实就行了。
代码
无重边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| #include<bits/stdc++.h>
using namespace std;
int dfn[111111], low[111111], scc[111111];
int scccnt, cnt, n, m;
bool vis[111111], flag[111111];
struct node
{
int v, idx;
};
vector<node> edges[111111];
stack<int> st;
int f[111111];
int ans;
void tarjan(int x, int fa)
{
vis[x] = 1;
f[x] = fa;
st.push(x);
cnt++;
dfn[x] = low[x] = cnt;
int ch = 0;
for (int i = 0; i < edges[x].size(); i++) {
int nex = edges[x][i].v;
if (!vis[nex]) {
ch++;
tarjan(nex, x);
low[x] = min(low[x], low[nex]);
if (low[nex] > dfn[x]) {
ans++;
flag[edges[x][i].idx] = 1;
}
} else if (nex != fa) {
low[x] = min(low[x], dfn[nex]);
}
}
return;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
edges[u].push_back({v, i});
edges[v].push_back({u, i});
}
for (int i = 1; i <= n; i++) {
if (!dfn[i]) {
tarjan(i, i);
}
}
vector<int> ans;
for (int i = 1; i <= m; i++) {
if (flag[i]) {
ans.push_back(i);
}
}
cout << ans.size() << '\n';
for (int i = 0; i < ans.size(); i++) {
cout << ans[i] << ' ';
}
return 0;
}
|
有重边
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| #include<bits/stdc++.h>
using namespace std;
int dfn[111111], low[111111], scc[111111];
int scccnt, cnt, n, m;
bool vis[111111], flag[111111];
stack<int> st;
int f[111111];
int ans;
struct node
{
int v, idx;
};
vector<node> edges[111111];
void tarjan(int x, int fa)
{
bool tp = 0;
vis[x] = 1;
f[x] = fa;
st.push(x);
cnt++;
dfn[x] = low[x] = cnt;
int ch = 0;
for (int i = 0; i < edges[x].size(); i++) {
int nex = edges[x][i].v;
if (!vis[nex]) {
ch++;
tarjan(nex, x);
low[x] = min(low[x], low[nex]);
if (low[nex] > dfn[x]) {
ans++;
flag[edges[x][i].idx] = 1;
}
} else if (nex != fa || tp) {
low[x] = min(low[x], dfn[nex]);
} else {
tp = 1;
}
}
return;
}
int main()
{
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
edges[u].push_back({v, i});
edges[v].push_back({u, i});
}
for (int i = 1; i <= n; i++) {
if (!dfn[i]) {
tarjan(i, i);
}
}
vector<int> ans;
for (int i = 0; i < m; i++) {
if (flag[i]) {
ans.push_back(i);
}
}
cout << ans.size() << '\n';
for (int i = 0; i < ans.size(); i++) {
cout << ans[i] << ' ';
}
return 0;
}
|
练习题
洛谷P3387
受欢迎的牛
UPD
2025.4.12 补充了一些东西
故意烦你


